Szerzők: Szenek Zoltán, Szám Donát

Elavult lenne már a zónázás?

A helyspecifikus gazdálkodás alapja, hogy a termőterület teljesítményének és a termesztett növények igényeinek megfelelően optimalizáljuk a tápanyagelosztást. Erre bevált módszer a zónák kijelölése. Nézzünk azonban a mélyére ennek, mert a zónázás előnyei közismertek, de a hibáiról szinte szó sem esett egészen mostanáig.

Mi lehet pontosabb egy zóna alapú tervezésnél és az ezen alapuló kijuttatásnál? Beállítottunk erre egy kísérletet és vissza is mértük a megvalósulást. Szokás szerint messzebbről indítjuk a gondolatmenetet, de ahogy megszokhattátok már tőlünk, így minden sokkal egyértelműbb lesz. Vágjunk is bele!

A precíziós mezőgazdaság a szántóföldi kultúrákban szinte egyet jelent a zóna alapú tervezéssel. Akkor mégis milyen hibája lehet?

Hogy erre választ kapjunk, ahhoz előbb vegyük szemügyre a jelentőségét és az előnyeit.

Mindent a szemnek, semmit a kéznek

Azzal nem mondunk sok újat, hogy a precíziós mezőgazdaság kőkeményen adatokon alapuló tervezést jelent. Itt már nem fér bele az, hogy tudod, hogy a táblád mely részein kell elzárni a műtrágyaszórót vagy manuálisan csökkenteni a dózist a monitoron. Egészen egyszerűen azért, mert szemmel nem lehet látni olyan szintű különbségeket, amikre mi már különálló zónákat tervezünk. Persze lehetnek extrém esetek, pl.: homokpadok az ahhoz képest sokkal jobb hozampotenciálú részek közé ékelve, ahol a traktorban ülve, menet közben is egyértelműen lehatárolható egy gyenge teljesítményű folt. Azonban kisebb eltérések garantáltan nem láthatók és főleg nem lehatárolhatóak mért adatok nélkül.

Ez volt a terméspotenciál, de mondunk egy másik példát, ami már a növény-egészségügy témakörébe tartozik. Színképelemzéssel (amilyen az NDVI is) olyan kezdődő betegségek jeleire is lehet következtetni, amiket ugyancsak nem látunk szabad szemmel. Műholdas, de még pontosabban drónos adatelemzéssel a visszavert fény minimális változásai is detektálhatók. Ezáltal a probléma azonosítható és a növényvédelmi kezelés még azelőtt megkezdhető, hogy szabad szemmel látható színelváltozás látszana a növényállományban.

Ezekből a rövid felvillantásokból is látható, hogy a gépek, az adatfelvevő- és adatelemző eszközök elengedhetetlen eszközei a modern mezőgazdasági tervezésnek. Ma már mindent mérni szükséges, hogy okszerű beavatkozásokat hajtsunk végre, legyen az tápanyagutánpótlás vagy növényvédelmi kezelés.

A helyspecifikus gazdálkodás előnyei már szinte az unalomig ismételtek, vizsgáljuk meg inkább ezeket kétféle szemszögből

A zóna alapú tervezés jelentősége és egyben nagy előnye abban rejlik, hogy a heterogén táblákon belüli eltérő teljesítményű területrészek lehatárolásával optimalizálható az inputanyagok kijuttatása. Ennek eredményeképpen a fajlagos termelési költségek a várható hozam megtartása mellett csökkenthetők.

Azonban nem csak így lehet megfogni a helyspecifikus gazdálkodás lényegét. A Gazdálkodó mondhatja azt is, hogy ő nem inputanyagot szeretne megspórolni, hanem a korábban alkalmazott összes szermennyiséget szeretné szétosztani a különböző teljesítményű zónákban, ahogy a bemutatásra kerülő táblánál is. Ennek eredményeként a várható hozamnövekedés révén többlethaszonra lehet szert tenni.

A zónák tervezése független attól, hogy melyik utat választja a Gazdálkodó, bármikor lehet belőle egyikre-másikra kijuttatási tervet készíteni. A lényeg az, hogy a mindenkori kijuttatás-tervezést megelőzően legyen leszögezve, hogy a várható hozam megtartása melletti inputanyag csökkentése vagy a várható hozam növelése melletti (korábban egy dózisban alkalmazott) inputanyag szétosztása a kívánatos.

A tervezéstől kezdve a kijuttatáson át a visszamérésig vegyünk végig egy táblát, hogy fény derüljön a klasszikus zónázás hibáira és arra, hogyan lehetne jobban csinálni.

Beállítottunk és vissza is mértünk erre egy kísérletet, hogy mindenre egyértelmű választ kapjunk, de haladjunk sorban.

Ha feltesszük a megfelelő kérdést, megkapjuk a megfelelő választ is

A domborzat jelentősen befolyásolja a hozamot, amely betudható a lejtőkön általában degradált talajminőségnek, a gyors lefolyás miatt irossz vízellátottságnak és a lejtőkitettségnek is. Precíziós talajvizsgálataink révén tudjuk, hogy sokszor néhány lépéssel alrébb, ahol élt vált a domborzat vagy csak kicsit megváltozik a lejtés, merőben eltérő talajösszetétellel találkozunk. Ez természetesen a hozam megváltozásával is jár.

A lejtőkön, így változatos domborzattal rendelkező táblákon mondanunk sem kell, hogy máshogy kell tervezni a zónákat és így a kijuttatási dózisokat is mint egy síkvidéki tábla esetében. Emiatt egy olyan táblát választottunk, amiben nincsenek lejtés nélküli területek és a térszíne is rendkívül szabdalt, különböző kitettségű lejtőkkel. A kiválasztási szempontoknál egyéb tényezőket is fegyelembe vettünk, de erről később. A tábla a Gerecsében található, Héreg határában.

A zónák tervezése összetett folyamat

A tábláról rendelkezünk 3 évi kalibrált hozamokkal, így ez egy nagyon jó kiindulóalapot jelent a tervezéshez. Az általunk kifejlesztett módszerrel a hozamadatok tisztítása után meghatároztuk az egyes évek relatív teljesítményét, majd ezeket is kiátlagoltuk egymással. Ennek eredményeképpen olyan térképet kaptunk, ami 3 év átlagát egyesíti egy térképben. A tervezés legkisebb egysége a 10×10 m kiterjedésű cella. Azért ezt a méretet választottuk, mert ez a Sentinel 2 műhold R-G-B-NIR csatornáinak felbontása is, amikből növényélettani indexek számíthatók. Minden mérési eredményünk ekkora és 30x30m-es cellákban egyedileg tárolódik. A későbbiekben ennek a méretválasztásnak még más jelentősége is lesz. A tábla területe 56,8 ha.

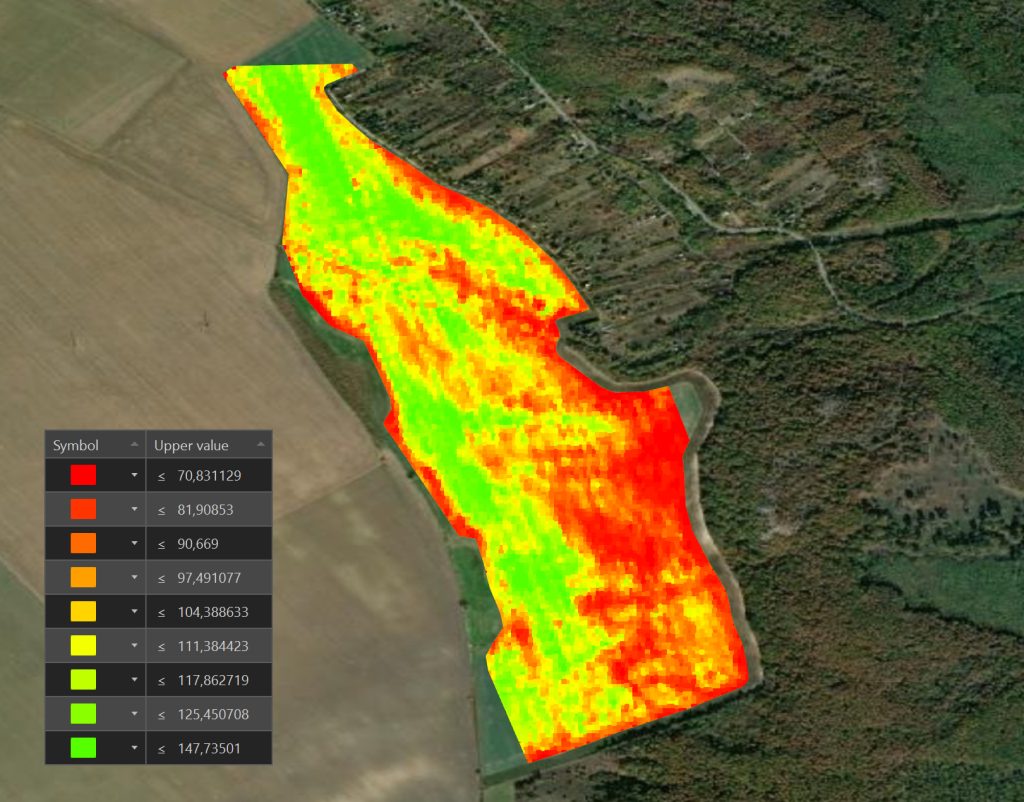
Gondolnánk, hogy ha megvan 3 év átlaga, akkor már lehet is zónákat kijelölni. Azonban ez messze nem így van, főleg nem változatos térszínnel rendelkező területeken. Ugyanis meg kell vizsgálnunk azt is, hogy mely területrészek mekkora lejtéssel rendelkeznek. Ennek azonban csak egy módja létezik.

A MePAR tartalmaz 12% és 17% lejtőkategóriatérképeket is, így magától értetődne, hogy ez alapján le lehet határolni a lejtőket. Azonban a gyakorlat teljesen mást mutat. Egyrészt a MePAR-ban lévő rétegek nem menthetőek ki téradatként a rendszerből, másrészt rendkívül pontatlanok, így nem alkalmasak a lejtők lehatárolására.

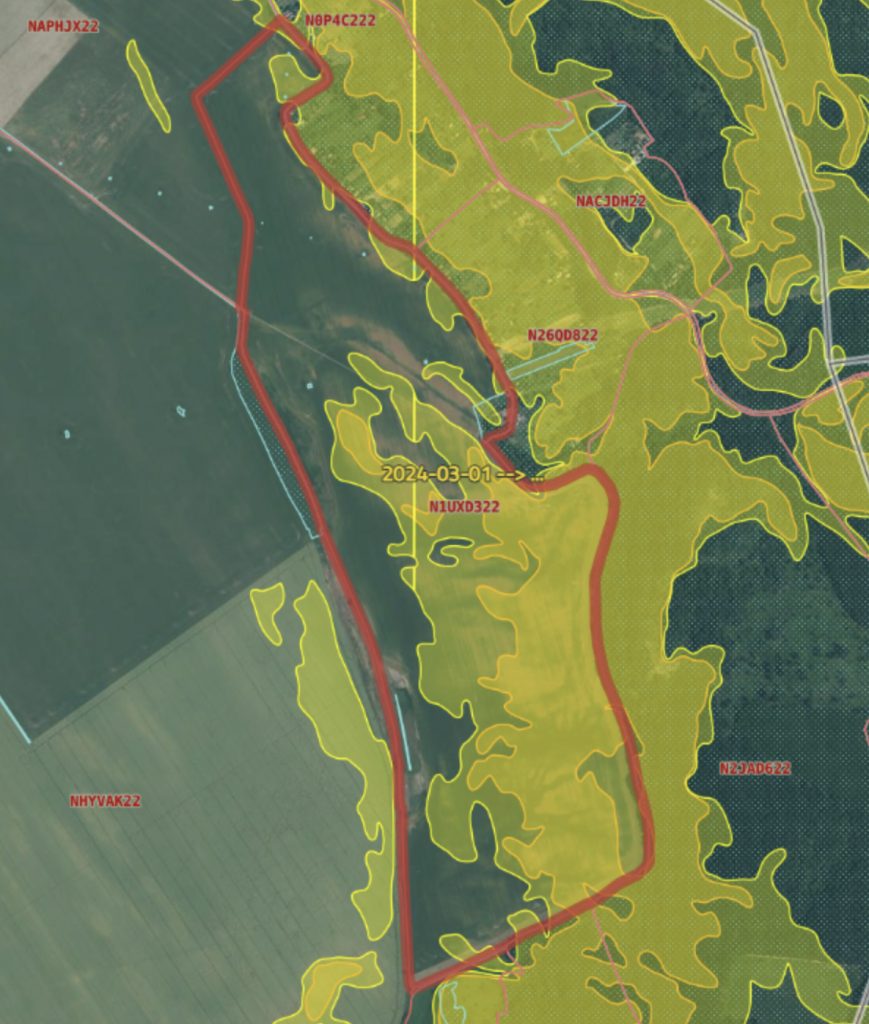
Nézzünk egy másik módszert. A hozamadatok és a visszamért kijuttatási adatok a klasszikus hozamtömegen felül tárolnak egyéb értékeket is. Többek között minden adatpont tartalmazza annak tengerszint feletti magasságát is. Azt gondolhatnánk, hogy ezek alapján meg lehet határozni a lejtők dőlésszögét és kitettségét. Azonban ez sincs így.

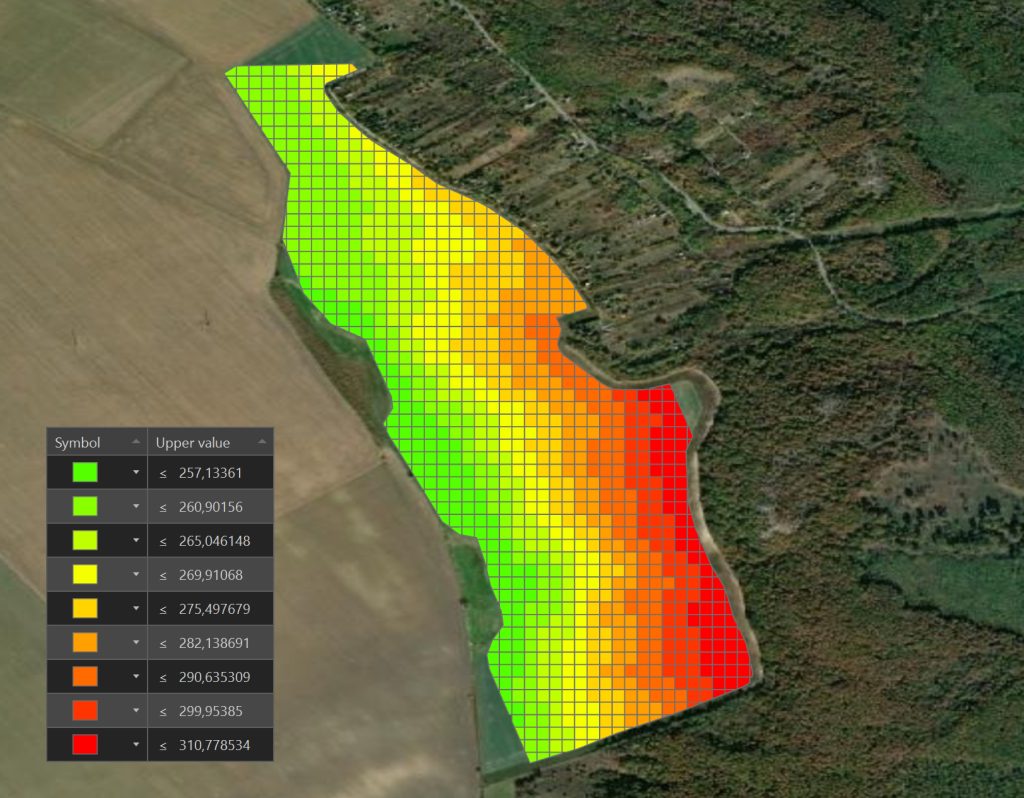
Ugorjunk vissza egy pillanatra a tábla madártávlati képéhez és hasonlítsuk össze a tengerszint feletti magassági eloszlással. Ez a térkép főként csak arról ad tájékoztatást, hogy mekkora magasságkülönbségek vannak a táblában és a tábla melyik égtáj felé lejt. Ebből tehát nem lehet tovább tervezni és lejtőszöget, főként nem lejtőirányt megállapítani. Akkor mi maradt nekünk?

Az egyetlen és pontos megoldást a monitoring drón jelenti. A területet lerepülve ugyanis megalkotható a tábla felületmodellje, amiből számítható a felszíni lefolyás, a lejtőszög és a lejtő kitettsége is.

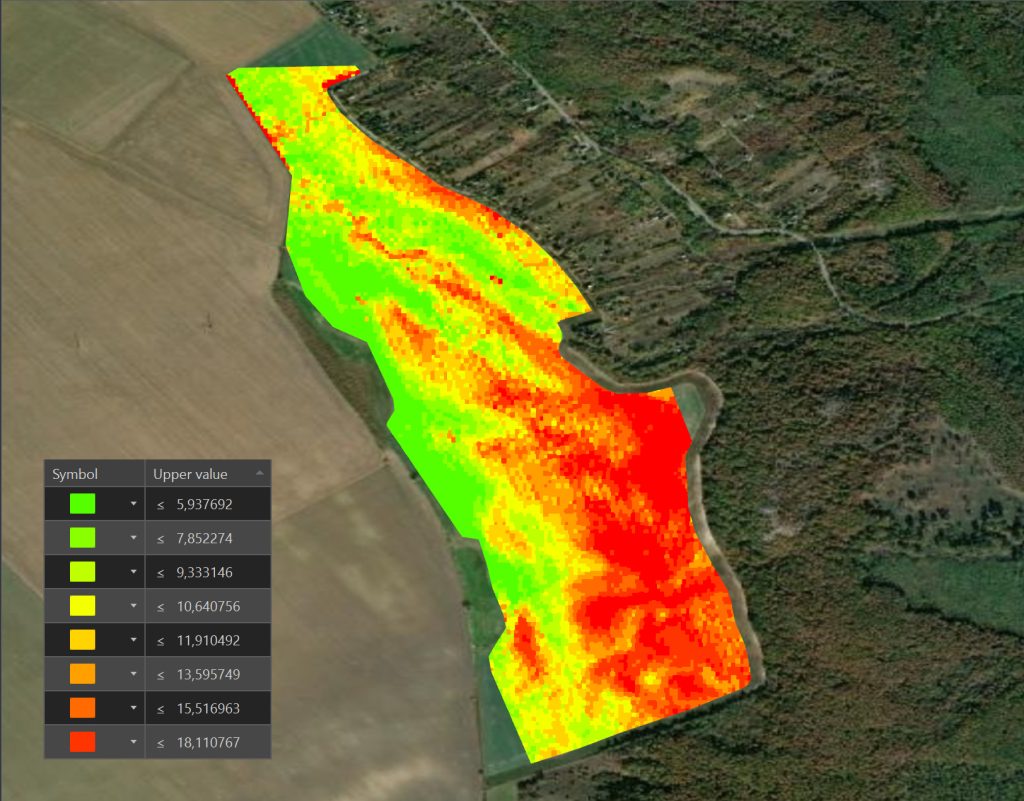
Érdemes megnézni, hogy mit mutat a raszteres, 13cm/pixel körüli felbontású drónfelvételből származtatott lejtőkategóriatérkép. A sötétvörös foltok jelölik a 17% és afeletti dőlésszögű lejtőket. Lényegesen kisebb területűek ezek mint ami a MePAR-ban van jelezve.

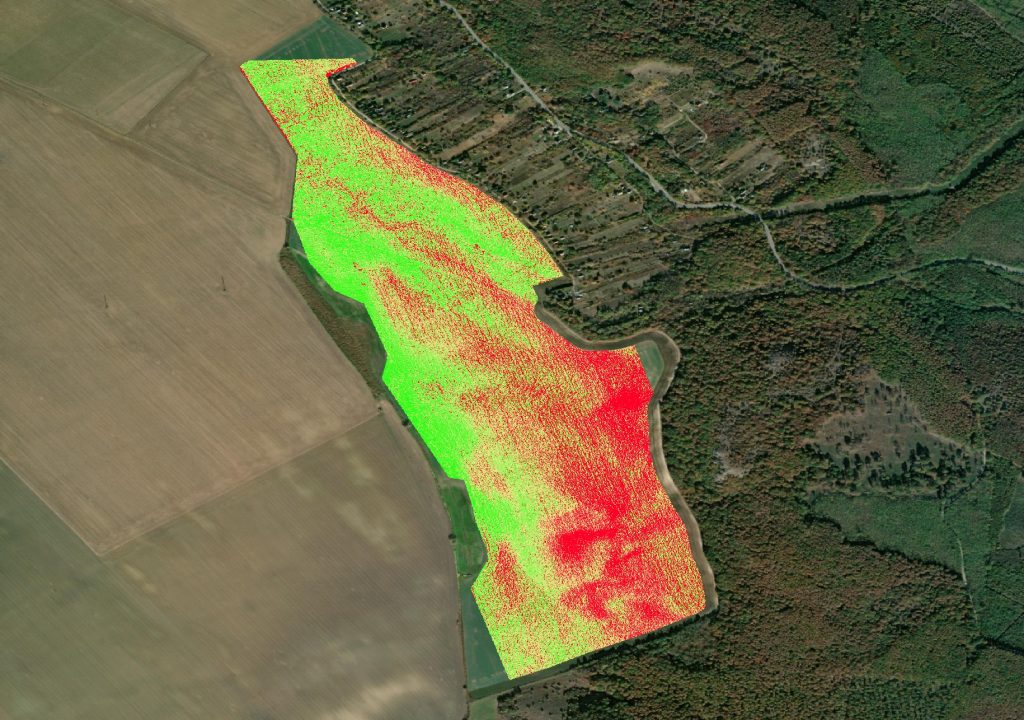
Ez a lejtőkategória térkép tehát hozzásegít minket ahhoz, hogy a zónákat a lejtőkkel pontosítsuk. Ez alapján már olyan zónákat állítottunk elő, ami alapján már kijuttatási dózisokat is tervezhetünk adott táblára szabottan.

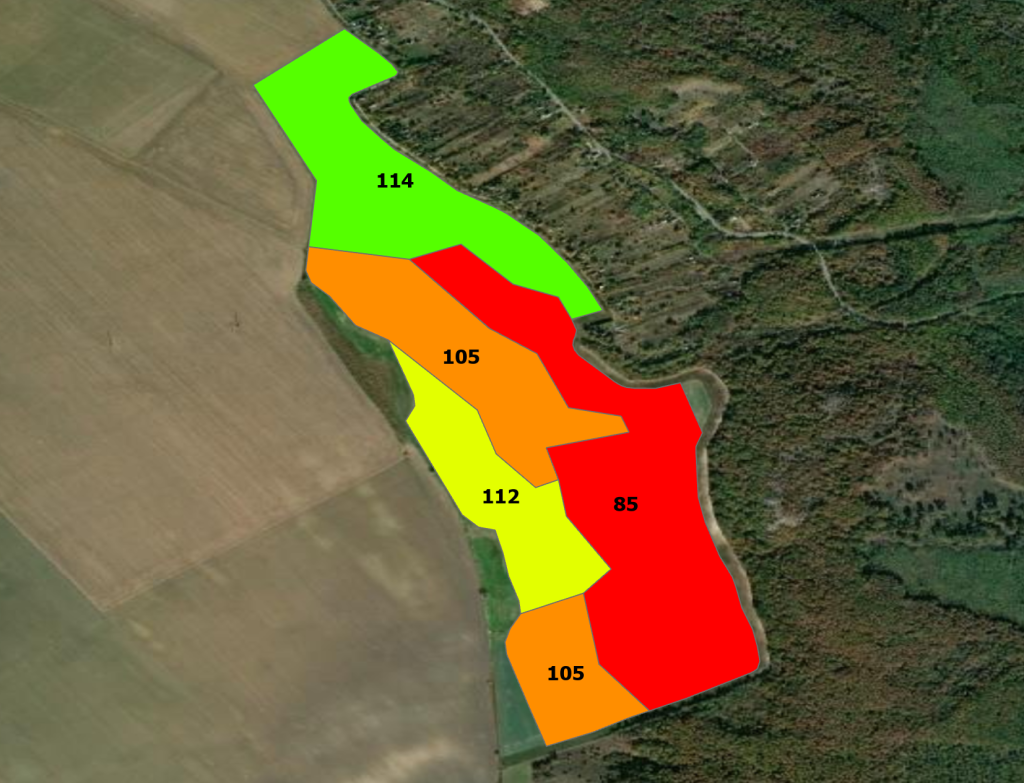
Kettőt egy csapásra

Jelen esetben a Gazdálkodó a korábban alkalmazott NPK tömeget kívánta kiszórni a táblára őszi búza elé, így nekünk ennek megfelelően kellett tervezni. Azáltal, hogy ezen a táblán nem történt mennyiség csökkentés, még nem jelenti azt, hogy ne lenne értelme differenciáltan tervezni. Nagyon nyomós okunk van rá, hogy megéri, sőt mindjárt kettő is!

A lejtőkategória térkép révén pontosan lehatárolhatóak a 17% és az afeletti lejtéssel rendelkező területek, ahova nem szabad kijuttatni N műtrágyát. Mint ahogy a korábbi képen már láthattuk, ezek a területek lényegesen kisebb kiterjedésűek mint ami a MePAR-ban látszik. Ez alapján tehát a tábla sokkal nagyobb területe műtrágyázható mint az a MePAR-ból kiolvasható.

A második ok már pénzügyi jellegű. A differenciált tervezés lehetővé teszi, hogy az átlagosnál jobban teljesítő területrészekre arányosan több műtrágyát tegyünk ki, míg a nagyobb lejtéssel rendelkező részeken a teljesítmény és a lejtés függvényében elvegyünk belőle. Ezáltal megmarad a korábban alkalmazott táblaátlag, de a várható hozam emelkedni fog és ráadásul a környezet- és természetvédelmi irányelveknek is megfeleltünk. Kettőt egy csapásra.

Az egy dózisú kijuttatással az 56,8 ha területű táblára 17.879 kg NPK műtrágya menne ki, míg a mi zóna alapú terveink alapján 17.989 kg. Ez 110 kg vagy 0,6% különbség, ami 0,35 ha területet jelent 315 kg dózissal számolva.

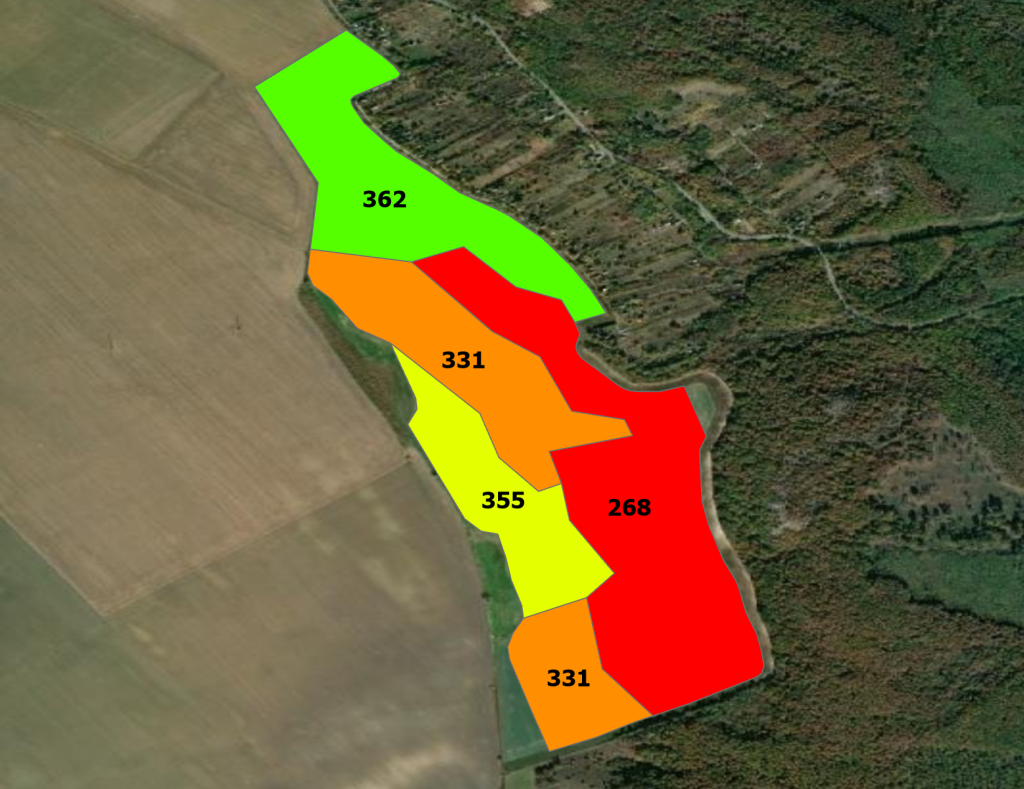
A legkisebb, oszthatatlan elemi zóna nyomában

Mint a képen is látható, 5 zónát határoltunk le a táblában. A legrosszabb és a legjobb teljesítményű zónák különbsége 29%, ami a degradált, lejtős területrészek figyelembevételével nem tűnik durván nagy különbségnek. Látható azonban, hogy az egységesnek tűnő zónákon belül is vannak eltérő teljesítményű területegységek, így érdemes lenne ezeket is tovább osztani. Azonban észre fogjuk venni, hogy ezeken a területeken belüli területeket is lehetne még tovább osztani, így zónázni. Ezzel pedig elérkezünk oda, hogy nem 5, hanem rengeteg zónánk lenne. Tehát az már látszik, hogy a zónákon belüli zónákon belüli zónák is kijelölhetőek, akkora változatossággal rendelkezik ez a tábla. Azonban ahelyett, hogy ezeket kézzel vagy valamilyen automatizmussal határolnánk le, létezik jobb megoldás is. Adná magát a dolog, hogy akkor menjünk le a 10×10 m-es rácsháló méretére és adjunk egyedi dózisokat minden elemi cellának annak a teljesítménye alapján. Azonban itt jön a képbe a munkagép “felbontása”.

A gazdaságban alkalmazott műtrágyaszóró 2×15 m szélességben terít, így nem lehet lemenni 30×30 m-es rácsméret alá a kijuttatásban. Mivel különféle gazdaságokban különféle szórási távolsággal rendelkező gépek vannak, így a tervezésnél mindig szükséges megvizsgálni a munkaszélességet is. A legkisebb tervezési egységet így felskáláztuk a 10×10 m-es rácsból egy 30×30 m-es rácsba. Ezt követően ezt tekintjük tervezési alapegységnek a legkisebb, tovább már oszthatatlan elemi zónának.

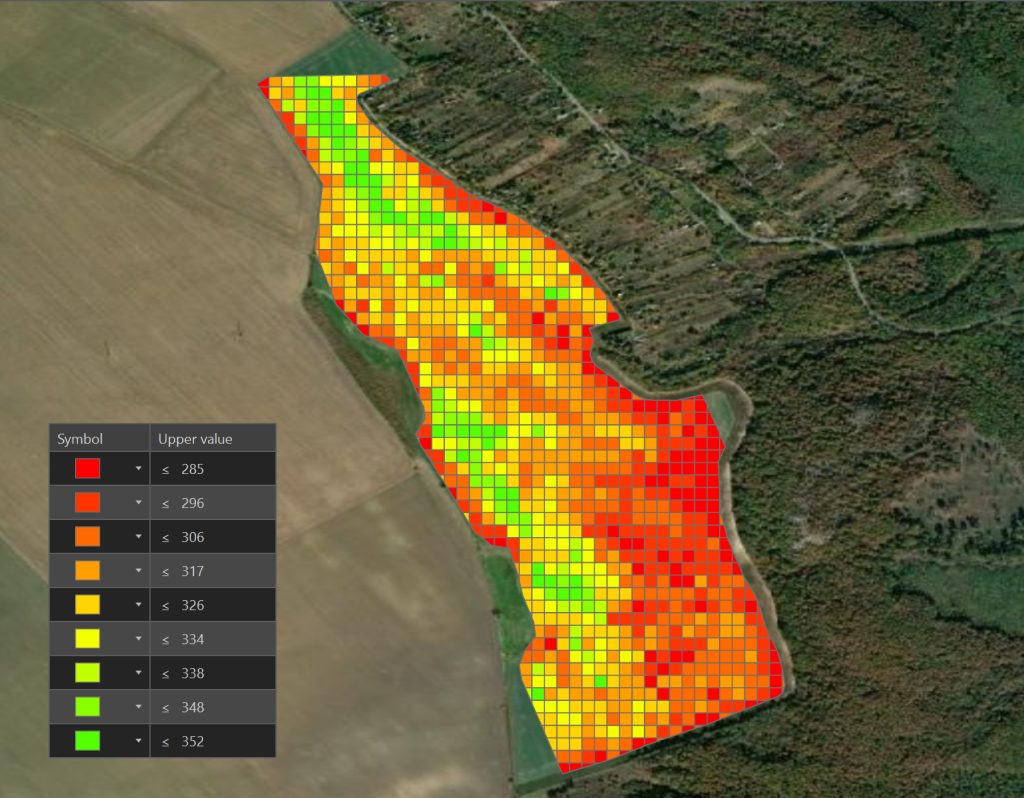
A képen is jól látszik, hogy mennyivel pontosabb kijuttatás válna ezáltal elérhetővé. Felmerül azonban egy fontos technikai kérdés: a műtrágyaszóró képes lekezelni ilyen pontossággal a dózisváltásokat és pontosan kimérni a kijuttatandó anyagmennyiséget? Hogy mindenkit előre megnyugtassunk, képes rá. Máskülönben nem lenne alkalmas precíziós kijuttatásra és lehetne visszavinni tömegével mindet a forgalmazónak, hogy ez így nem precíziós.

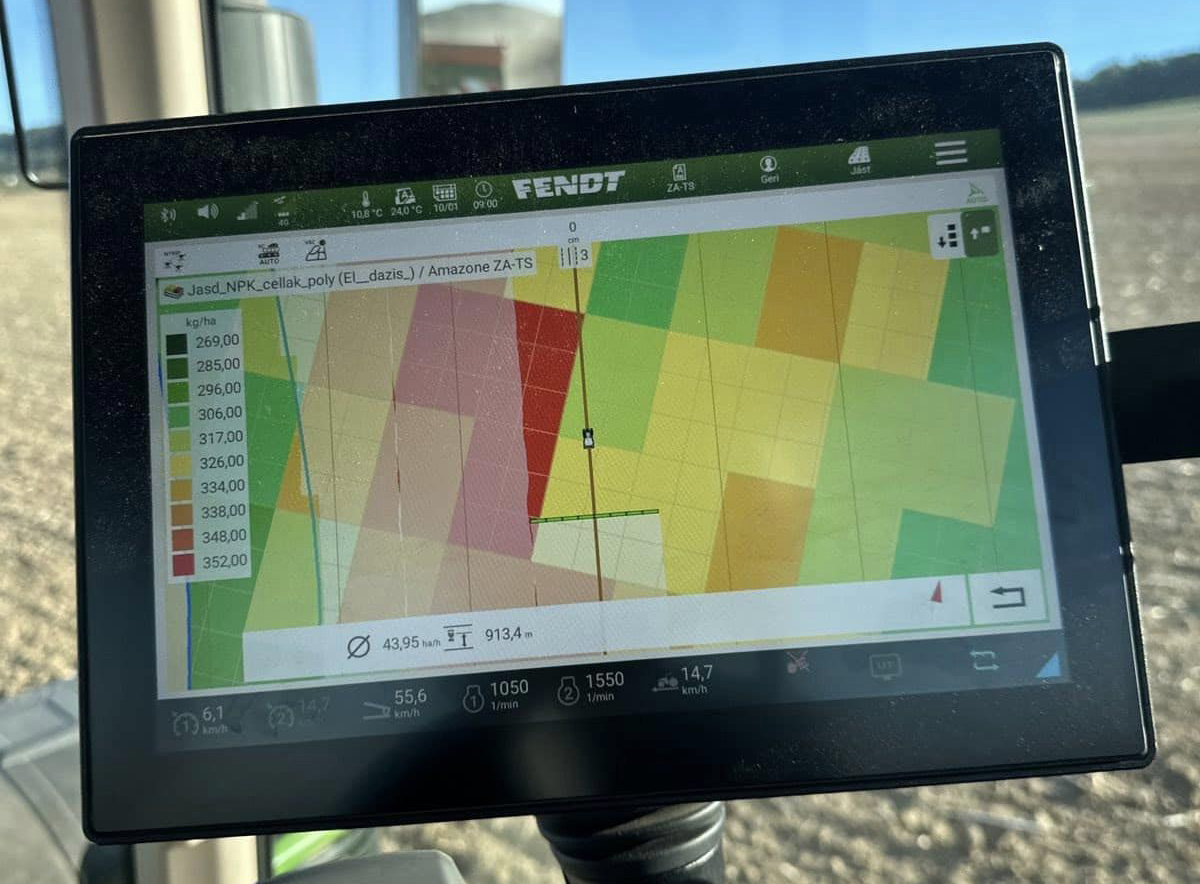
A cellaméret felskálázása miatt a 8555 cellából 1038 jön létre 88 különféle dózissal. Itt megint felmerül egy következő technológiai korlát, ugyanis a Gazdaságban alkalmazott Fendt traktor nem tud ennyiféle különböző dózist lekezelni, így ezekből 9 dózisosztályt hoztunk létre.

Mindezek után az 1038 cella 9 különféle dózisátlaga pontosan 315 kg átlagdózist eredményez, ami a korábbi, egy dózisú konvencionális kezelésnek megfelelő mennyiség. A teljes műtrágyatömeg pedig 17.960 kg. Emlékeztetőként, az egy dózisú 17.879 kg lenne. Erre az eltérésre már nem is számolunk hibát, mert 5% alatt amúgyis elenyésző.

Összevetve a zóna alapú kijuttatással, a cellás kijuttatástól azt várjuk, hogy sokkal jobban leköveti a domborzatot és így a talajerő változásait mint a zónás módszer, ami által sokkal pontosabb tápanyagutánpótlás valósítható meg. Arra tehát választ kaptunk, hogy hogyan lehetne jobban csinálni. A gépek alkalmasak rá, a korlátaikat ismerjük, a dózisokat beállítottuk. Jöhet a kijuttatás és annak a visszamérése!

Papíron vagyis esetünkben tervezési térképen a cellás NPK kijuttatás hatékonyabb a zónás módszernél. Mit mutat a gyakorlat?

Muszáj lelőnünk: működik. Nem is akármilyen hatékonysággal. Az eredmények bemutatása után egyből még tovább megyünk és olyan összefüggéseket is megmutatunk, amiket még garantáltan nem láthattál!

A kijuttatás probléma nélkül lezajlott, kaptunk képeket a kijuttatásról. Ezeken a képeken is látható, ahogy a traktor a függesztett műtrágyaszóróval végighalad a 30×30 m-es cellákon. Az egyes cellákon áthaladáskor vált a dózis, nem keletkezik hibaüzenet és szórási szélességben menti az útvonalat, hogy ne történjen felülkezelés.

Az egy dolog, hogy mit láttunk, a lényeg, hogy a traktor mit mér

Mint minden elvégzett munkaműveletet, így a differenciált műtrágyaszórást is rögzíti és menti a traktor monitora. Ezek az adatok nagyon hasonlóak a hozamadatokhoz, tehát pontszerű, geolokációval ellátott adatpontok. Ezek szórási szélességben keletkeznek, tehát 30 méteres sorokban találhatóak egymástól a traktor útvonala mentén. Sűrűségük ezáltal sokkal kisebb mint a hozamadatok esetében, de azokhoz hasonlóan sokrétű információt tartalmaznak.

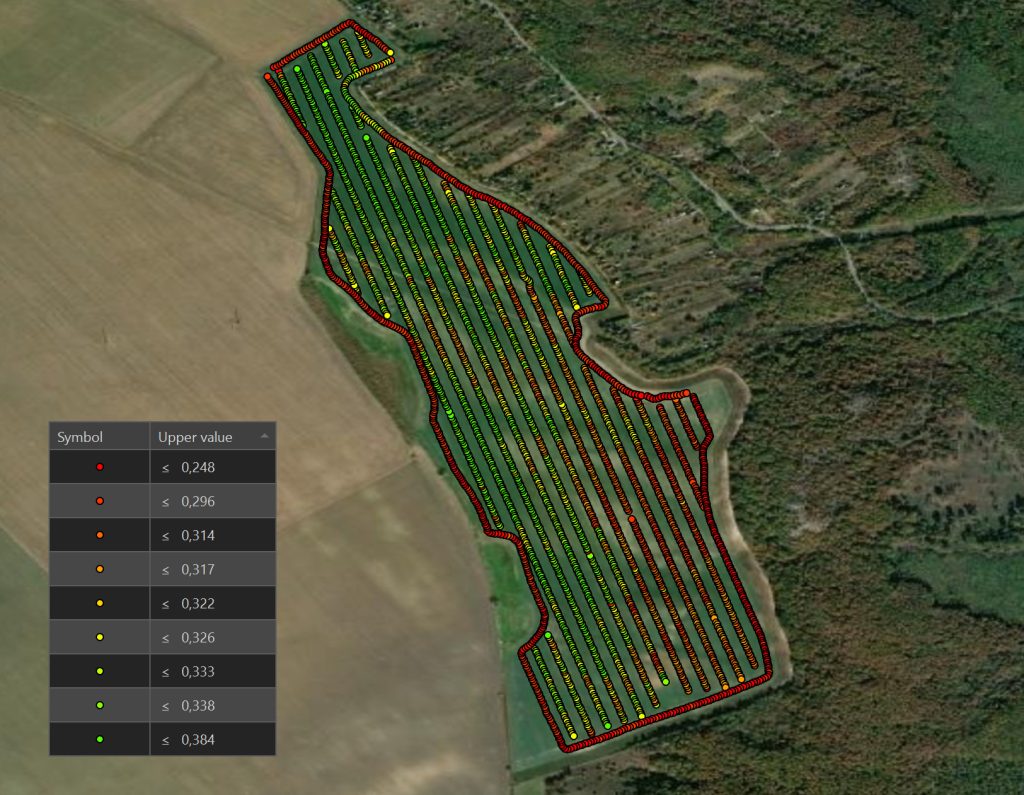
Fontos, hogy az adatletöltés a traktor monitorából pendrive segítségével történjen, mert a felhőben tárolt, továbbított és lementett adatok nem a teljes adattömeget tartalmazzák. Technológia fejlődés ide vagy oda, a teljes, nyers adattartalom eléréséhez még mindig ezt a módszert kell alkalmazni. Megéri azonban így lementeni az adatokat, kulcsfontosságú összefüggésekre lehet szert tenni. Nem szükséges minden munkamenet után ezt megtenni, elegendő évente néhányszor, miután egy nagyobb munkaművelet sorozat lezajlott.

Ugyanúgy mint a hozamadatok esetében, itt is szükség van az adatok megtisztítására, mert tartalmaznak valótlan értékeket is. Az adatok tisztítását mindkét esetben ugyanazzal a módszerrel végeztük. Összesen 3815 adatpont keletkezett, amelyből 70 bizonyult hibásnak, ami 2%-on belüli érték. Mivel az adatpontok mennyisége kevesebb mint a hozamadatok esetében, így kevesebb hibás adatpont is keletkezik. Azonban feltétlen szükséges ezt megtenni, mert nagyban befolyásolja a mérési eredményeket. Ez a 70 hibás adatpont 1,2%-al vinné el a hibaarányt, ami nem tűnik soknak, de jelentősen befolyásolja az adatok közötti összefüggések részletes feltárását.

Mit mutat a szórási kép?

Azt már tudjuk, hogy a kijuttatás pontossága bőven hibahatáron belül van. Most nézzük meg, hogy milyen lett a szórási kép, tehát hogyan követte le a műtrágyaszóró a tervezett cellákat.

A tervezési előírás szerint összességében 17.960 kg NPK-t kívántunk kijuttatni. A visszamért, tisztított, interpolált térkép összességében 17.560 kg műtrágya kijuttatást detektált. Ez 2,2% különbség, ami 1,3 ha-nak felel meg, 315 kg/ha-al szórva. Itt muszáj megjegyeznünk, hogy a mellette lévő, szintén változatos térszínnel rendelkező táblában a zóna alapon kijuttatott MAS szórás hibája 1,6% volt.

Ez a hiba annak fényében főként elenyésző, hogy a műtrágyaszórónak is van bizonyos fokú hibája, a traktorral le kell követni a folyamatos domborzatváltást és a cellák között is állandóan váltani kell a dózisokat. Egy teljes cellában max. 7-8 másodperc alatt halad át a traktor és a dózisváltás késleltetés nélkül és pontosan történik.

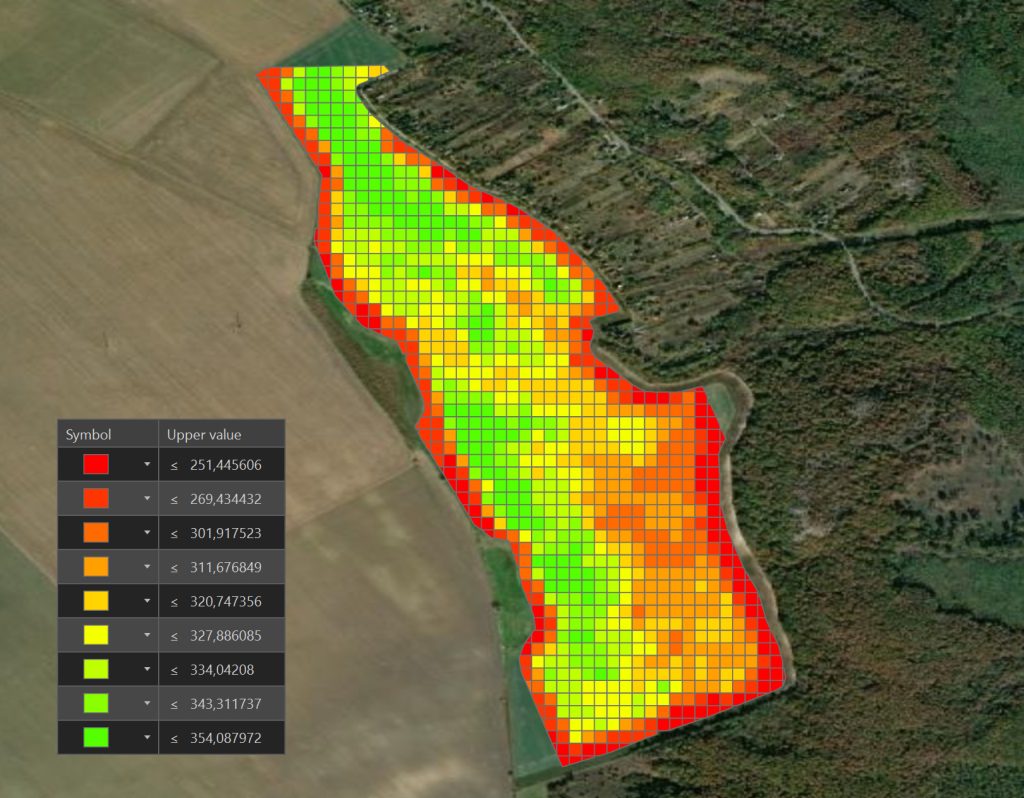
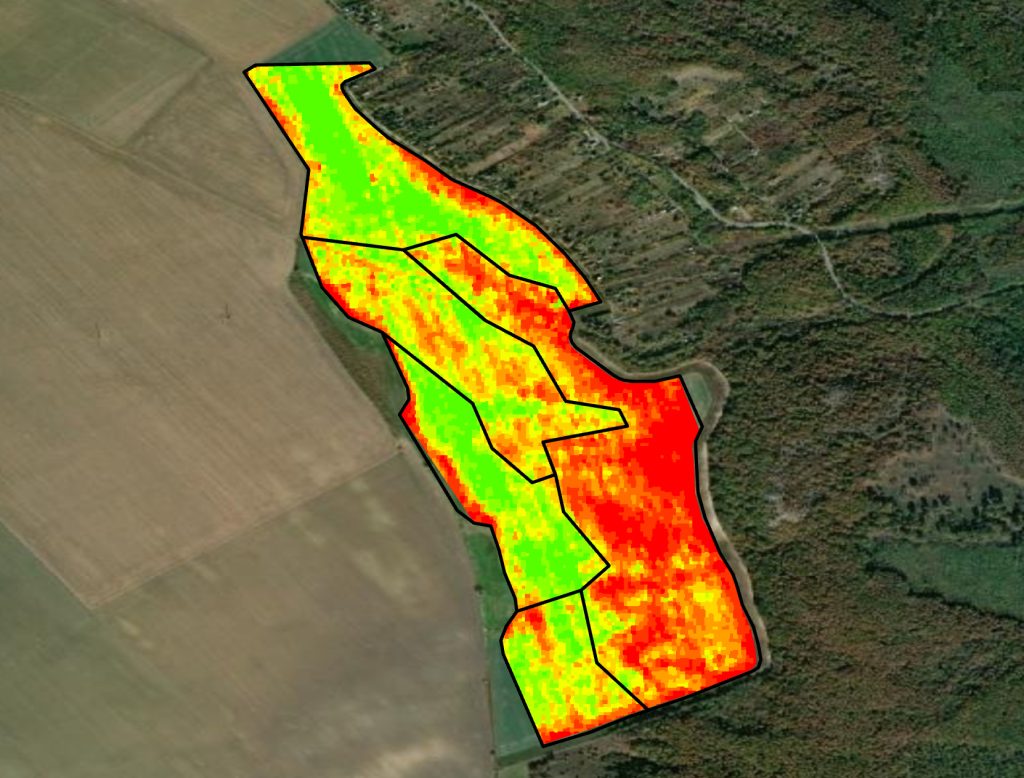
A szórási kép magáért beszél, a domborzat változásait szinte szinte tökéletesen lekövette, amire zónás kijuttatással nem lenne lehetőség. A következő képre ráillesztettük a zónákat is, hogy látható legyen, mekkora különbségek vannak zónán belül is. Ahogy már korábban is beszéltük, a zónák kijelölése nem hibás, mert ezekkel egyértelműen meghatározhatók az eltérő tulajdonságú területek, hanem egész egyszerűen a klasszikus zónázási módszerrel nem lehet elkülöníteni olyan kis területegységeket, amik ezt le tudnák követni.

A módszer korlátai

Kutatásunk nem arról szól, hogy innentől kezdve felejtsük el a zónázást, ez már elavult és váltsunk a cellás módszerre. Ugyanúgy beszélni fogunk a korlátairól és hibáiról is. Nézzük előbb a módszer korlátait.

A zónák kijelölése főként több évi hozamadatok kiátlagolásán alapul és soha nem lesz két egymáshoz nagyon hasonló hozamtérkép. Emiatt a zónák tartalmaznak magterületeket, amiket nagy bizonyossággal ki lehet jelölni és pufferterületeket, amik évről évre változni fognak. Azért választottuk ezt a táblát kísérletünk helyszínéül, mert rendkívül szabdalt a domborzat egyenetlenségei által és a lejtőkön a degradált talaj miatt viszonylag azonos teljesítményt tudnak az egyes területegységek.

Tehát ez a módszer nem alkalmazható olyan táblákban, amikben a hozamadatok évről évre markáns eltéréseket jeleznek, mert nem biztosítható a következetes tápanyagutánpótlás. Ilyen, változatos domborzattal és markáns, minden évben hasonlóan teljesítő területegységekkel rendelkező táblákban viszont van értelme.

A módszer hibái

Ahogy a képen is látható, nem minden cella kapta meg a saját értékét, akkor miért jó mégis a szórási kép és miért mondjuk, hogy jobban megéri mint a zónás módszer?

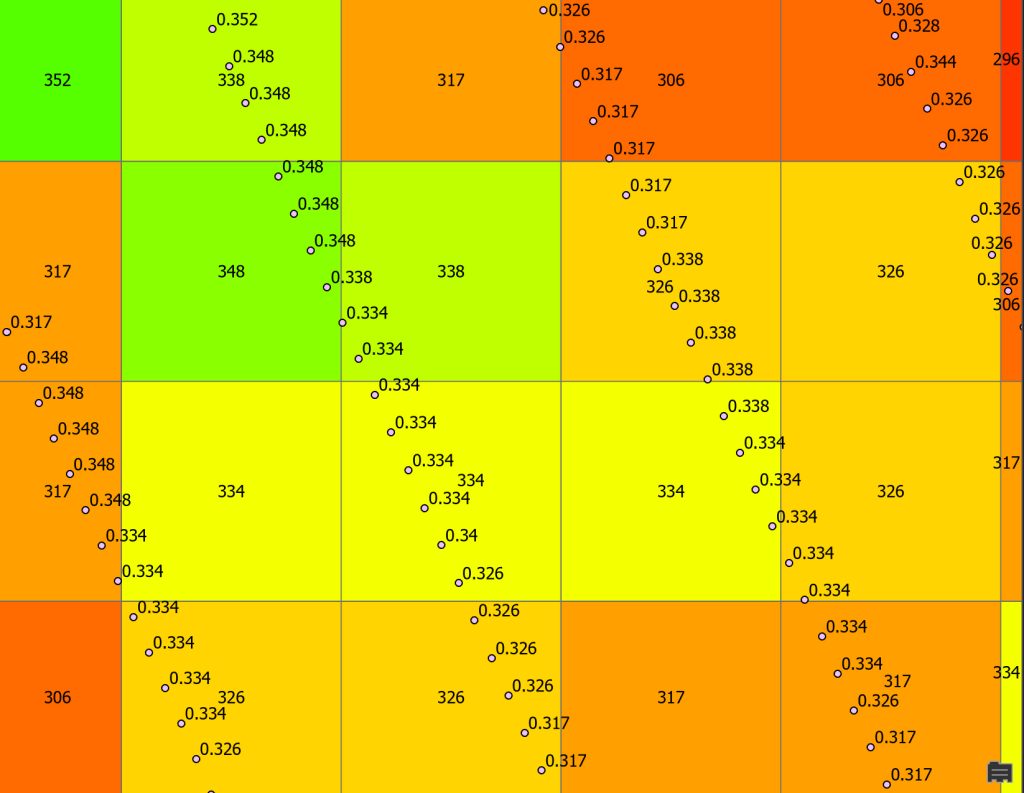
Az ellentmondás feloldása egyszerű elven alapul. A szórótárcsa mindkét irányba 15-15 méter szélességben terít, ezért úgy érzékeli mintha képzeletben egy 30 méteres szórókeret lenne a függesztett műtrágyaszóró helyén. Hiába állítottuk be a rácsot a szórási szélességre, lesznek olyan pontok, amikor több cellában tartózkodik egyszerre és ekkor azt a dózist szórja ki, aminek az értéke nagyobb és amelyikben legalább 51% átfedéssel tartózkodik. Ez kijuttatóeszközönként változhat, de a lényeg az, hogy mindig a szomszédos cellák értékét veszi alapul, így nem szór teljesen rossz értékeket. A dózisváltások azonnal megtörténnek, átmenet nélkül és mindig a megadott értékeket veszik fel a szomszédos cellákon belül.

A kijuttatóeszköz ezen hibája ellenére is képes lekövetni a domborzatot és pontosan kiszórni a megfelelő mennyiséget. De ez csak megfelelő méretű táblákban működik jól.

Ha csak néhány munkamenet szélességű a tábla, akkor nem feltétlenül működik és nem is feltétlenül kell ott ezt a módszert erőltetni, ahogy a korlátainál is láthattuk.

Most pedig jöjjenek az extra megfigyelések, mert ezzel még nincs vége az elemzésnek!

Nézzük meg, hogy miket lehet kihozni a monitoring drónrepülés adataiból, mert a táblahatár kijelölésén túl sokkal többet is és még csak NDVI dróm sem kell hozzá!

Domborzatmodellezés drónnal

Korábban már említettük, hogy még a hozamadatokból álló sűrű adatpontfelhő sem elegendő ahhoz, hogy domborzatmodellt alkossunk egy tábláról. De miért olyan fontos ez?

A drón nem leíró adatokat rögzít mint a traktorok és a kombájnok, hanem lencsék által alkotott klasszikus képet készít, amik esetünkben geolokációval ellátottak. Ez azt jelenti, hogy a kamera felbontásától, a repülési magasságtól és a légkör tisztaságától függően centiméteres nagyságrenddel rendelkező felbontású képeket rögzít. Ezekből a képekből pedig digitális domborzatmodell építhető fel, amiből lejtőszög és lejtőirány is számítható.

A korábbiakban ismertetett, lejtőszögeket ábrázoló képen látható, hogy mennyire pontosan leköveti a hozam a domborzat változásait. Ez egy olyan stabil, független változó, ami jelentős mértékben meghatározza a talajminőséget, így befolyásolja a hozamot. Ennek a térképnek és a következő vizsgálatoknak a felbontása már nem 30x30m, hanem visszaálltunk a műholdak által meghatározott 10x10m-es rácsra. A miértre egy másik cikkünkben esik majd szó, ami már a mítoszrombolás kategóriáját fogja erősíteni. Térjünk vissza most azonban ahhoz a gondolathoz, hogy a lejtőszög milyen mértékben hat a hozamra.

Ahol az excel véget ér, ott kezdődik a célszoftverrel történő elemzés

Az excel alkalmas alapösszefüggések feltárására, azonban mi szeretnénk mélyebbre ásni és egyéb, fontos összefüggéseket is feltárni.

Ezen a ponton megkértük Tóth Rebekát, aki az adatelemző vonalat képviseli, hogy tárja fel nekünka lejtőszög és a hozam között fennálló részletesebb összefüggéseket. Innentől az ő elemzését és szavait tolmácsoljuk szó szerint. Elsőre nagyon szakmainak tűnhet, de mindezek a lépések és vizsgálatok kellenek ahhoz, hogy egzakt végeredményt kapjunk. Mondanunk sem kell, hogy maximálisan elégedettek vagyunk a munkájával és a mérések igazolják sejtéseinket, nem is akármilyen mértékben.

SPSS-ben a függő (dependent) és a független (independent) változók közötti kapcsolatok elemzését végeztem el. A függő változó az, amit meg szeretnénk jósolni vagy vizsgálni, és amit befolyásolhatnak más tényezők. Jelen esetben a „hozamteljesítmény”. A független változók pedig azok, amelyek potenciálisan befolyásolják a függő változót. Ami itt a „lejtőszög” lesz.

Tehát a független változót használjuk arra, hogy megmagyarázzuk vagy előre jelezzük a függő változó viselkedését.

Lépések:

• normál eloszlás ellenőrzése
• korrelációelemzés
• lineáris regresszió

A korreláció elemzés elvégzéséhez szükséges a normál eloszlás vizsgálata. A pontosság végett a korreláció elemzéshez szükséges tudnunk, hogy az adatok normál eloszlásúak-e, a megfelelő módszert kiválasztása szempontjából.

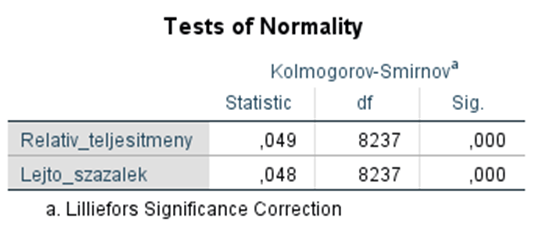
Normál eloszlás teszt eredménye:

Az adatok mennyisége (n=8237) volt a döntő abban, hogy a Kolmogorov-Smirnov teszttel folytassam az elemzést, ami szerint mind a lejtő_százalék, mind a relatív_teljesítményhozam esetében a szignifikancia értéke (Sig.) 0.000.

A szignifikancia szint azt jelenti, hogy milyen valószínűség mellett utasítjuk el a nullhipotézist (ami ebben az esetben az, hogy az adat normál eloszlású).

Az Sig. (p-érték) mutatja az eredményt:

• Ha a p-érték kisebb, mint 0.05, akkor a változó nem normál eloszlású.
• Ha a p-érték nagyobb, mint 0.05, akkor a változó normál eloszlású.

Ez azt jelenti, hogy az adatok nem követik a normál eloszlást. Emiatt alkalmazzuk a Spearman-féle rangkorrelációt, amely nem követeli meg a normál eloszlást.

A továbbiakban a Spearman korrelációt (nem érzékeny az eloszlás formájára) használtam a hozamteljesítmény és a lejtőszög közötti kapcsolat feltárására.

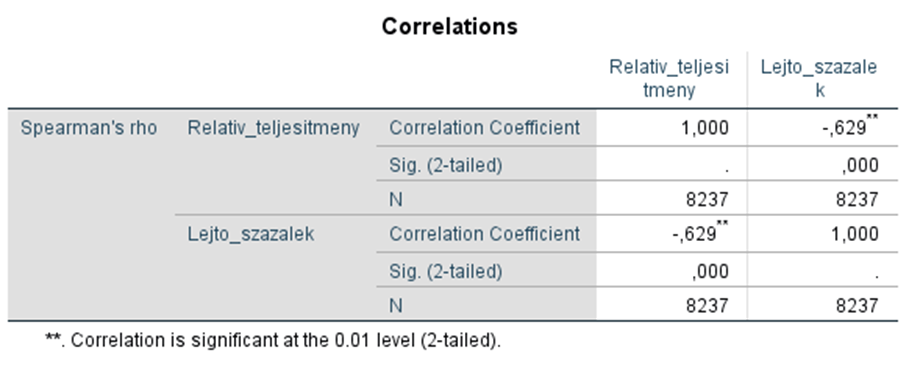
Korrelációs elemzés:

A Spearman-féle rangkorreláció eredménye azt mutatja, hogy a két változó közötti korreláció (r érték) -0.629, ami azt jelenti, hogy erős negatív kapcsolat áll fenn a lejtőszázalék és a relatív teljesítményhozam között.

Az előjel (+ vagy -) az irányt jelzi:

• +: Pozitív kapcsolat (pl. a lejtőszög növekedése esetén a hozamteljesítmény is nő).
• -: Negatív kapcsolat (pl. a lejtőszög növekedésével a hozamteljesítmény csökken).

Értelmezés:

• 0 – 0.3: Gyenge korreláció.
• 0.3 – 0.5: Közepes korreláció.
• 0.5 – 1: Erős korreláció.

Az r érték mindig -1 és +1 között van:

• +1: Tökéletes pozitív lineáris kapcsolat (ha az egyik változó növekszik, a másik is mindig növekszik).
• -1: Tökéletes negatív lineáris kapcsolat (ha az egyik változó növekszik, a másik mindig csökken).
• 0: Nincs lineáris kapcsolat a változók között.

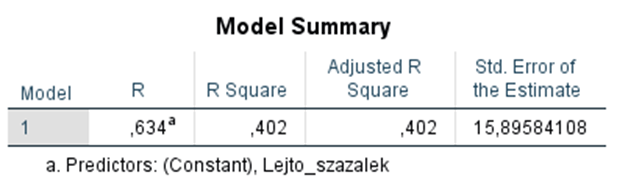
Regressziós eredmények:

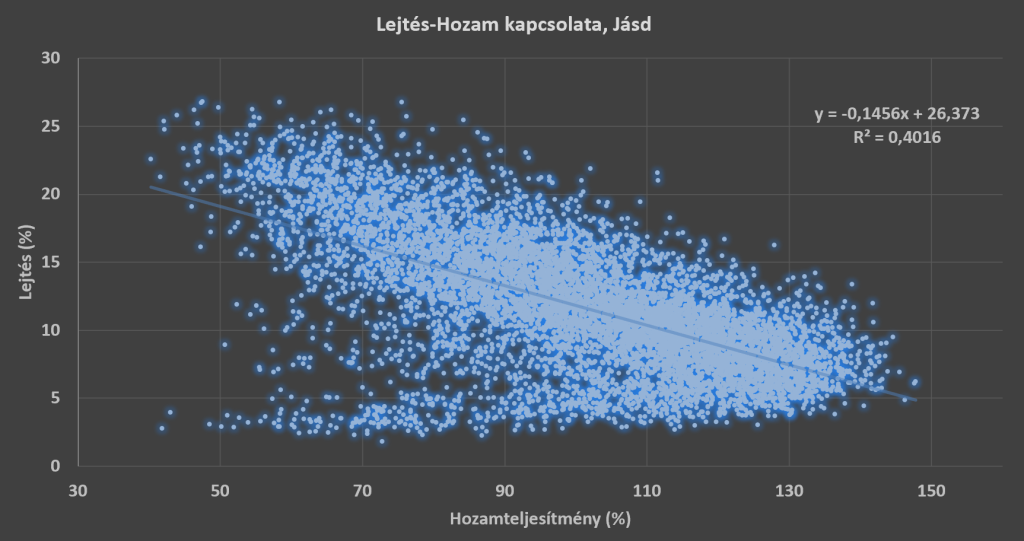
Az R-négyzet(R Square) értéke 0.402, ami azt jelenti, hogy a lejtőszázalék a relatív teljesítményhozam varianciájának 40,2 %-át magyarázza.

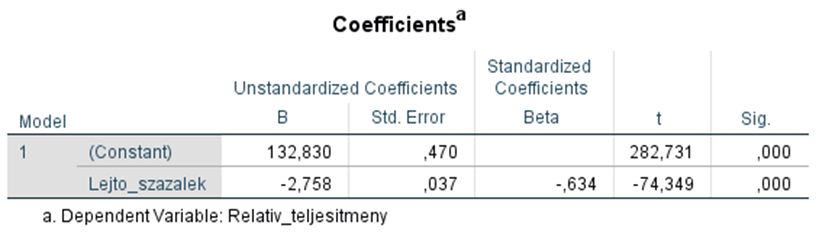
 Együtthatók és az eredmények értelmezése:

A lejtő_százalék együtthatója (B) -2.758, ami azt jelenti, hogy a lejtő meredekségének 1%-os növekedése a relatív teljesítményhozamot átlagosan 2.758%-kal csökkenti. Ez egy lineáris kapcsolatot feltételez, ahol minden egyes egységnyi növekedés a lejtő meredekségében azonnal és arányosan csökkenti a hozamot.

Összefoglalva

Az elemzés alapján egy erős, szignifikáns negatív kapcsolatot kaptam a terület lejtő százaléka és a relatív teljesítményhozama között. Az eredmények világosan mutatják, hogy a lejtő meredekségének növekedése jelentősen rontja a hozamot, és ezt a kapcsolatot a lineáris regresszió eredményei is megerősítik. A modell erős alapot nyújt a következtetésekhez, de további tényezők bevonásával további részleteket is feltárhatunk.

A lejtőkitettségnek a szántóföldön is van hatása?

A következetes, pontos és minden részletre kiterjedő vizsgálat eredménye számszerűsítve is megmutatta nekünk, hogy milyen jelentősen befolyásolja a lejtőszög a hozamteljesítményt.

Azonban menjünk még tovább és nézzük meg, hogy a lejtő kitettsége, tehát iránya hogyan befolyásolja a hozamteljesítményt?!

Látható, hogy a drónrepülésből származó adatokból nem csak a lejtőszög, hanem a lejtő iránya is kiszámítható, így összevethető válik a lejtő kitettségének a hozamteljesítményre gyakorolt hatása is!

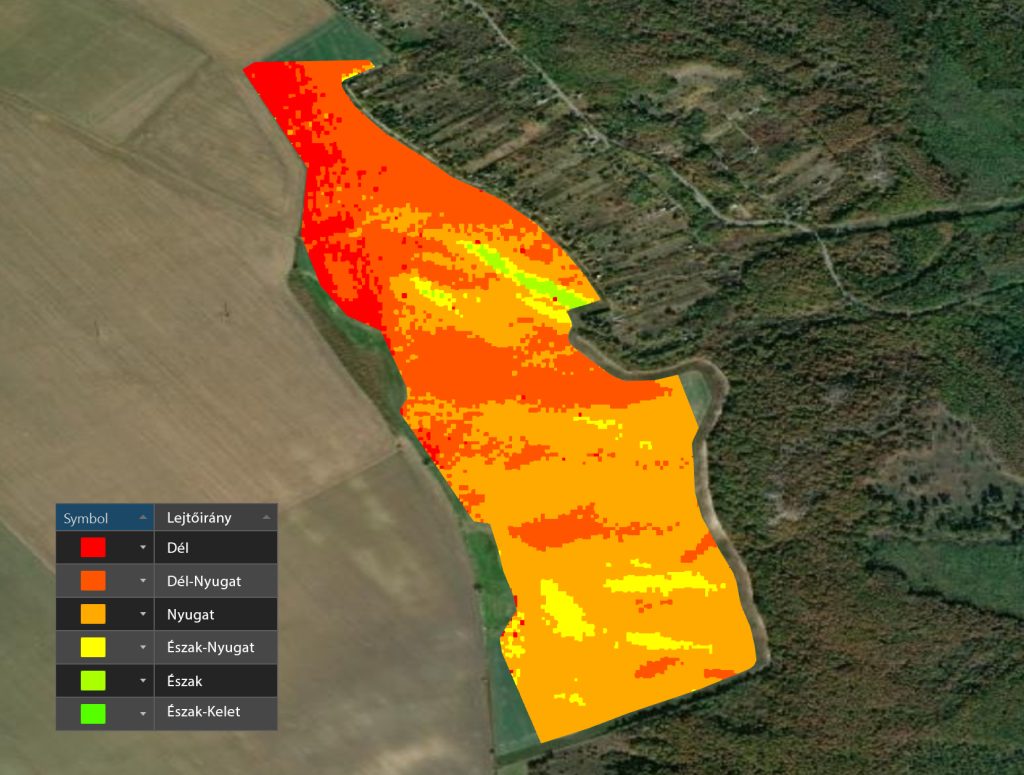
A képen jól látható, hogy a tábla lejtőinek legnagyobb része, 54%-a Ny-i tájolású, 33%-a DNy-i, 7 %-a D-i, 5%-a ÉNy-i, míg 1%-a É-i. A teljesítményüket tekintve a D-i tájolású területek teljesítenek a legjobban átlagosan 108%-kal, majd ezt követi a DNy-i 106 %-kal, az ÉNy-i 98%-kal és a sort az É-i és a Ny-i tájolású lejtők zárják 97%-kal.

Nem meglepő, hogy az É-i féltekén a D-i és a DNy-i tájolású lejtők jobban teljesítenek mint az É-i, ÉNy-i és Ny-i lejtők. 11% különbség nem tűnik soknak, de ez a tábla 8 tonna körül teljesít búzából, ami a kedvezőtlen kitettségű lejtőkön 7 tonna körüli értékre redukálódik. A tábla 40%-a tagolódik a kedvező kitettségű lejtőirányokra, tehát nagyon is számít, hogy a lejtés függvényében persze, de a megfelelő mennyiségű tápanyag kerüljön kijuttatásra, mert a kedvezőtlen kitettségű területetek hozamát felhozni már csak a földrajzi adottságok miatt sem lehet.

Végső következtetésként meg kell válaszolnunk a címben feltett kérdést, miszerint: elavult lenne már a zónázás?

Vannak olyan esetek, amikor a cellás kijuttatás pontosabb eredménnyel jár mint a zónás. Azonban olyan esetekben, amikor évről-évre kiegyensúlyozatlanul teljesít egy tábla, még mindig a zóna alapú kijuttatás a biztosabb módszer. Mi a helyzet a folyékony kijuttatással? Nos ez egy másik, izgalmas kutatás témája lesz.

A weboldalunkon található dokumentumok, adatok felhasználását, letöltését, másolását Cégünk nem engedélyezi. A weboldallal összefüggésben, ill. a weboldalon található egyes elemeken fennálló szerzői jogokat és a szellemi alkotáshoz fűződő jogokat köteles minden látogató tiszteletben tartani. A weboldal dokumentumai, anyagai szerzői jogi védelem alatt állnak és azok bármilyen, engedély nélküli használata, másolása, letöltése, felhasználása jogszabályba ütközik.